Série 6
Fonctions (2)
But
Le but de cette série d'exercices est de vous faire pratiquer encore plus les fonctions en C++ : prototypage, définition, surcharge, valeurs par défaut, récursivité.
Création du projet sous QTCreator
Afin de vous inciter à vous familiariser avec QTCreator, une façon simplifiée de configurer cet outil vous est proposé dans cette série. Inspirez-vous de la vidéo de la semaine passée en utilisant cette fois l'archive serie6.zip.
Exercice 1 : Surcharge de fonction (niveau 1)
(pages 32 et 212 dans la 2e édition).
- vous copiez la fonction echange de l'exercice 4 de la semaine passée ;
- vous définissez deux autres fonctions de même nom, l'une qui échange les valeurs de variables de type double et l'autre pour des valeurs de type char.
int main()
{
int i(10), j(55);
char a('B'), b('a');
double x(3.14159), y(1.414);
cout << "Avant: i=" << i << " et j=" << j << endl;
echange(i,j);
cout << "Après: i=" << i << " et j=" << j << endl << endl;
cout << "Avant: a=" << a << " et b=" << b << endl;
echange(a,b);
cout << "Après: a=" << a << " et b=" << b << endl << endl;
cout << "Avant: x=" << x << " et y=" << y << endl;
echange(x,y);
cout << "Après: x=" << x << " et y=" << y << endl;
return 0;
}
Avant: i=10 et j=55 Après: i=55 et j=10 Avant: a=B et b=a Après: a=a et b=B Avant: x=3.14159 et y=1.41 Après: x=1.41 et y=3.14159
Exercice 2 : Factorielle (fonctions récursives, niveau 1)
Pour calculer n! (factorielle n), on peut utiliser deux formules différentes :
-
La formule itérative :
n! = 1 * 2 * 3 * ... * n -
La formule récursive définissant
n!
en fonction de (n-1)! :
0! (factorielle de zéro) = 1 pour tout entier n>0, n! = n * (n-1)!
Implémentez ensuite la fonction :
unsigned int factorielleIterative(unsigned int n)
unsigned int désigne un entier non signé. Utilisez simplement ce type tel quel, nous aurons l''occasion d'y revenir dans un prochain cours.
Dans le même fichier, implémentez la fonction:
unsigned int factorielleRecursive(unsigned int n)
[Remarque : Le corps de la fonction tient en 5 lignes]
En réutilisant la fonction demander_nombre déjà utilisée plusieurs fois dans les séries précédentes, écrivez, dans la fonction main, le programme qui demande à l'utilisateur d'entrer un entier naturel n (entre 0 et 12 si vous utilisez des int ou des long et entre 0 et 20 si vous utilisez des long long int), et affiche n! en faisant une première fois appel à factorielleIterative, puis dans un second temps à factorielleRecursive.
Pour terminer, on pourra ajouter une boucle demandant à l'utilisateur s'il souhaite recommencer.
Exemple de déroulement
Entrez un nombre entier compris entre 0 et 12 : 12
Méthode itérative :
12! = 479001600
Méthode récursive :
12! = 479001600
Voulez-vous recommencer [o/n] ? o
Entrez un nombre entier compris entre 0 et 12 : 6
Méthode itérative :
6! = 720
Méthode récursive :
6! = 720
Voulez-vous recommencer [o/n] ? n
Exercice 3 : Nombres de Fibonacci (fonctions récursives, niveau 1)
Les nombres de Fibonnaci sont définis par la suite :
F(0) = 0 F(1) = 1 F(n) = F(n-1)+ F(n-2) avec n>1
Le but de cet exercice est d'écrire un programme qui calcule la valeur de F(n) selon la définition récursive précédente.
Dans le fichier fibonacci.cc, prototypez puis définissez la fonction
unsigned int Fibonacci(unsigned int n)
Pour comparaison, voici une manière itérative (i.e. non récursive) de calculer les n premier termes de la suite :
unsigned int FibonacciIteratif(unsigned int n)
{
unsigned int Fn(0); // stocke F(i) , initialisé par F(0)
unsigned int Fn_1(Fn); // stocke F(i-1), initialisé par F(0)
unsigned int Fn_2(1); // stocke F(i-2), initialisé par F(-1)
for (unsigned int i(1); i <= n; ++i) {
Fn = Fn_1 + Fn_2; // pour n>=1 on calcule F(n)=F(n-1)+F(n-2)
Fn_2 = Fn_1; // et on decale...
Fn_1 = Fn;
}
return Fn;
}
Note : la méthode récursive est coûteuse en temps de calcul (elle est «exponentielle»), ne lancez pas le calcul pour des nombres trop élevés (disons supérieurs à 40).
Exemple de déroulement
Entrez un nombre entier compris entre 0 et 40 : 0
Méthode itérative :
F(0) = 0
Méthode récursive :
F(0) = 0
Voulez-vous recommencer [o/n] ? o
Entrez un nombre entier compris entre 0 et 40 : 1
Méthode itérative :
F(1) = 1
Méthode récursive :
F(1) = 1
Voulez-vous recommencer [o/n] ? o
Entrez un nombre entier compris entre 0 et 40 : 2
Méthode itérative :
F(2) = 1
Méthode récursive :
F(2) = 1
Voulez-vous recommencer [o/n] ? o
Entrez un nombre entier compris entre 0 et 40 : 3
Méthode itérative :
F(3) = 2
Méthode récursive :
F(3) = 2
Voulez-vous recommencer [o/n] ? o
Entrez un nombre entier compris entre 0 et 40 : 7
Méthode itérative :
F(7) = 13
Méthode récursive :
F(7) = 13
Voulez-vous recommencer [o/n] ? n
Exercice 4 : Calcul approché d'une intégrale (niveau 2)
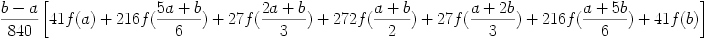
Ecrivez un programme calculant cette valeur approchée. Pour cela écrivez 3 fonctions :
-
Une fonction f de votre choix, qui
corresponde à la fonction dont vous souhaitez calculer l'intégrale.
(Essayez plusieurs cas avec x2, x3, ..., sin(x), 1/x, etc. Il faudra bien sur recompiler le programme à chaque fois.)
(Pour utiliser les fonctions mathématiques, n'oubliez pas d'ajouter «#include <cmath>» en début de programme.
Pour plus de détails, voir la section correspondante dans la mini-référence sur les fonctions) - Une fonction integre qui, à partir de deux arguments correspondant à a et b, calcule la somme ci-dessus pour la fonction f ;
- Une fonction qui demande à l'utilisateur d'entrer un nombre réel. S'en servir pour demander les bornes a et b de l'intégrale.
Entrez un nombre réel : 4 Entrez un nombre réel : 5 Integrale de f(x) entre 4 et 5 : 20.3333333333 Entrez un nombre réel : 0 Entrez un nombre réel : 9.5 Integrale de f(x) entre 0 et 9.5 : 285.791666667 Entrez un nombre réel : -1.5 Entrez un nombre réel : 200.3 Integrale de f(x) entre -1.5 et 200.3 : 2678685.80067Pour la fonction f(x)=1/x:
Entrez un nombre réel : 4 Entrez un nombre réel : 5 Integrale de f(x) entre 4 et 5 : 0.223143551349 Entrez un nombre réel : 0 Entrez un nombre réel : 9.5 Integrale de f(x) entre 0 et 9.5 : inf Entrez un nombre réel : 12 Entrez un nombre réel : 45 Integrale de f(x) entre 12 et 45 : 1.32199884499
Vous pouvez également utiliser intégrateur en ligne de https://www.wolframalpha.com/calculators/integral-calculator pour vérifier d'avantage de résultats.
Note : Vous pourrez trouver ici une démonstration de la formule [lien externe] donnée plus haut.
 |
Remarque : | |
|
Comment faire pour ne pas recompiler le programme pour chaque nouvelle fonction ?
En tant que tel, c'est-à-dire laisser l'utilisateur saisir lui-même
sa formule, cela est beaucoup trop compliqué pour ce cours d'introduction. |
Exercice 5 : Fonctions logiques (niveau 3)
On vous donne la fonction non_et :
bool non_et(bool A, bool B)
{
return not(A and B);
}
bool non(bool A) bool et(bool A, bool B) bool ou(bool A, bool B)
Commencez par écrire la fonction non à l'aide de non_et. Vous pouvez alors utiliser la fonction non en plus de non_et pour écrire la fonction et. La fonction ou peut s'écrire en utilisant les fonctions non et et.
Exercice 6 (LIEN PARTIE THÉORIQUE) : Recherche dichotomique (fonctions récursives, niveau 2)
Les algorithmes récursifs et de recherche dans une collection vont être abordés formellement dans la partie théorique. En attendant, nous faisons une petite incursion sur le plan pratique.
Pour illustrer l'utilisation de la récursivité dans la recherche d'un élément dans une liste ordonnée, nous allons jouer à un petit jeu :
Pensez très fort à un nombre entre 0 et 100...
voilà !
L'ordinateur doit maintenant le trouver...
Principe
Pour ce faire, il pourrait énumérer tous les nombres les uns après les
autres jusqu'à avoir la bonne réponse.
Mais, vous en conviendrez aisément, ce n'est pas une méthode très efficace...
Une autre méthode (plus efficace) est la méthode dite « par dichotomie » : on réduit le champ de recherche à chaque étape et on recommence la recherche sur le nouvel intervalle.
On commence avec la zone complète, puis on choisit un pivot (point central de la zone de recherche). En fonction de la comparaison de ce pivot avec l'élément recherché, plusieurs cas de figures peuvent se présenter:
- on a trouvé le bon élément -> il suffit de le retourner
- le pivot est plus grand que l'élément recherché -> on recommence la recherche sur le domaine délimité par le pivot (à gauche)
- le pivot est plus petit que l'élément recherché -> on recommence la recherche sur le domaine débutant par le pivot (à droite)

Mise en pratique
Dans le fichier dichotomie.cc
-
Prototypez et définissez la fonction :
de sorte qu'elle effectue la recherche dans l'intervalle [borneInf, borneSup]
unsigned int cherche(unsigned int borneInf, unsigned int borneSup);
Cette fonction devra choisir un pivot au milieu de l'intervalle (ou s'arrêter, avec un message d'erreur, si l'intervalle est vide), proposer le pivot à l'utilisateur, puis en fonction de sa réponse (<, > ou =) s'appeler elle-même sur le nouvel intervalle ainsi déterminé, ou arrêter la recherche.
La fonction retourne la valeur trouvée (ou la borne inférieure en cas d'erreur).
-
Dans la fonction main, demandez à l'utilisateur
de choisir (dans sa tête) un nombre entre 1 et 100 (définissez deux
constantes MIN et MAX).
Cherchez la solution à l'aide le la fonction cherche puis affichez le résultat trouvé.
Exemple de déroulement
Pensez à un nombre entre 1 et 100. Le nombre est il <, > ou = à 50 ? < Le nombre est il <, > ou = à 25 ? > Le nombre est il <, > ou = à 37 ? < Le nombre est il <, > ou = à 31 ? > Le nombre est il <, > ou = à 34 ? < Le nombre est il <, > ou = à 32 ? > Le nombre est il <, > ou = à 33 ? = Votre nombre était 33.
Exercice 7 : Devoir 4 du MOOC (niveau 2)
Les devoirs du MOOC, même s'il ne sont pas notés pour vous, sont un bon moyen de vous entraîner, notamment en vue du mini-projet et de l'examen. Vous pouvez les soumettre à un correcteur automatique (autant de fois que vous le souhaitez) et recevoir un feedback. Le devoir de la semaine 4 vous entraîne à l'utilisation de fonctions.