Série 4
Boucles conditionnelles et itérations
But
Le but de cette série d'exercice est de vous faire pratiquer les boucles conditionnelles et les itérations en C++.Préliminaires :
Rappelez-vous le fonctionnement de ces séries : elles ont des niveaux et le but n'est pas de tout faire. Revoir si nécessaire les instructions à ce sujet données la semaine passée.
Par ailleurs, remarquez qu'il n'est pas nécessaire d'imprimer
systématiquement les séries; la forme électronique (dans votre navigateur) permet d'utiliser les
liens, ainsi que le copier-coller avec le bouton central de la souris.
De plus, si vraiment vous préférez lire un énoncé sur papier, vous avez tout intéret
à utiliser le livre d'exercices C++ par la pratique;
vous gagnerez un temps considérable pendant les TPs en évitant d'imprimer les
séries et votre lecture sera facilitée par la mise en page nettement plus soignée
(vous bénéficierez en plus des ajouts qu'offre le livre par rapport aux séries).
Création du projet sous QTCreator
Afin de vous inciter à vous familiariser avec QTCreator, une façon simplifiée de configurer cet outil vous est proposé dans cette série. Suivez cette petite vidéo en utilisant l'archive serie4.zip pour voir comment procéder.
Exercice 1 : Les tables de multiplication (itération for, niveau 1)
Objectif
Écrivez un programme tables.cc affichant les tables de multiplication de 2 à 10.
Votre programme devra produire la sortie suivante à l'écran :
Tables de multiplication Table de 2 : 1 * 2 = 2 ... 10 * 2 = 20 ... Table de 5 : 1 * 5 = 5 2 * 5 = 10 ... ... Table de 10 : 1 * 10 = 10 ...
Méthode :
Utilisez deux structures d'itération for imbriquées l'une dans l'autre.
Exercice 2 : Rebonds de balles (itération for, niveau 2)
Objectif :
L'objectif de cet exercice est de résoudre le problème suivant :
Lorsqu'une balle tombe d'une hauteur initiale h, sa
vitesse à l'arrivée au sol est
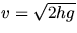 .
Immédiatement après le rebond, sa vitesse est v1=eps*v (où eps
est une constante et v la vitesse avant le rebond).
Elle remonte alors à la hauteur
.
Immédiatement après le rebond, sa vitesse est v1=eps*v (où eps
est une constante et v la vitesse avant le rebond).
Elle remonte alors à la hauteur
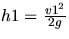 .
.
Le but est d'écrire un programme (rebonds1.cc) qui calcule la hauteur à laquelle la balle remonte après un nombre nbr de rebonds.
Méthode :
On veut résoudre ce problème, non pas du point de vue formel (équations) mais par simulation du système physique (la balle).
Utilisez une itération for et des variables v, v1, (les vitesses avant et après le rebond), et h, h1 (les hauteurs au début de la chute et à la fin de la remontée).
Tâches :
Écrivez le programme rebonds1.cc qui affiche la hauteur après le nombre de rebonds spécifié.
Votre programme devra utiliser la constante g, de valeur 9,81 et demander à l'utilisateur d'entrer les valeurs de
- H0 (hauteur initiale, contrainte : H0 >= 0),
- eps (coefficient de rebond, contrainte 0 <= eps < 1)
- nbr (nombre de rebonds, contrainte : 0 <= NBR).
Essayez les valeurs H0 = 25, eps = 0.9, NBR = 10. La hauteur obtenue devrait être environ 3.04.
Remarque :
-
Pour utiliser les fonctions mathématiques (comme sqrt()),
ajoutez
#include <cmath> au début de votre fichier source.
Exercice 3 : Rebonds de balles - le retour. (boucles do...while, niveau 2)
(pages 21 et 203 dans la 2e édition).
On se demande maintenant combien de rebonds fait cette balle avant que la hauteur à laquelle elle rebondit soit plus petite que (ou égale à) une hauteur donnée h_fin.
Écrivez le programme rebonds2.cc qui affiche le nombre de rebonds à l'écran.
Il devra utiliser une boucle do...while, et demander à l'utilisateur d'entrer les valeurs de :
- H0 (hauteur initiale, contrainte : H0 >= 0),
- eps (coefficient de rebond, contrainte 0 <= eps < 1)
- h_fin (hauteur finale désirée, contrainte : 0 < h_fin < H0).
Essayez les valeurs H0=10, eps=0.9, h_fin=2. Vous devriez obtenir 8 rebonds.
Exercice 4 : Nombres premiers (structures de contrôle, niveau 2)
Écrivez le programme premier.cc qui demande à l'utilisateur d'entrer un entier n strictement plus grand que 1, puis décide si ce nombre est premier ou non.
Algorithme :
-
Vérifier si le nombre n est pair (si oui, il n'est pas premier sauf si c'est 2).
Pour tous les nombres impairs inférieurs ou égaux à la racine carrée de n, vérifier s'ils divisent n. Si ce n'est pas le cas, alors n est premier.
Tâches :
Si n n'est pas premier, votre programme devra afficher le message: "Le nombre n'est pas premier, car il est divisible par D ", où D est un diviseur de n autre que 1 et n.
-
Sinon, il devra afficher le message: "Je crois fortement que ce nombre est premier".
Testez votre programme avec les nombres : 2, 16, 17, 91, 589, 1001, 1009, 1299827 et 2146654199. Indiquez ceux qui sont premiers.
Les résultats devraient ressembler à ceci :
2 est premier 16 n'est pas premier, car il est divisible par 2 17 est premier 91 n'est pas premier, car il est divisible par 7 589 n'est pas premier, car il est divisible par 19 1001 n'est pas premier, car il est divisible par 7 1009 est premier 1299827 est premier 2146654199 n'est pas premier, car il est divisible par 46327
Exercice 5 : Une histoire de prêt (boucle, niveau 2)
L'objectif de cet exercice est de résoudre le problème suivant :
Une banque prête une somme S0 à une personne X. Chaque mois, X rembourse un montant r (sur la somme empruntée) et paye par ailleurs (en plus) un intérêt ir*S, où S est la somme restant à rembourser (avant déduction du remboursement mensuel).
Quelle est la somme des intérêts encaissés par la banque quand X a remboursé la totalité de son prêt ?
Écrivez le programme pret.cc qui calcule la somme des intérêts encaissés et la durée en mois du remboursement, puis qui affiche ces informations à l'écran !
Contraintes :
- Votre programme devra utiliser une boucle while.
- Les valeurs S0, r et ir seront demandées à l'utilisateur avec les contraintes : S0 >= 0 , r > 0, et 0<=ir<1.
Testez votre programme avec les valeurs suivantes : S0=30000, r=1200, ir=0.01 (i.e. 1%). La somme des intérêts encaissés (sur 25 mois) est alors de 3900.
Exercice 6 : Suite et série (niveau 2)
a) Écrivez un programme qui calcule les 10 premiers termes de la suite Un telle que:
| U0 = 1, Un+1 = | Un |
| n+1 |
U0 = 1
U1 = 1
U2 = 0.5
U3 = 0.1666667
U4 = 0.0416667
U5 = 0.0083333
U6 = 0.0013889
U7 = 0.000198413
U8 = 2.48016e-5
U9 = 2.75573e-06
U10 = 2.75573e-07
b) Modifiez votre programme pour qu'il calcule simultanément la suite Un et la série Vn, où
| Vn = | n | Ui . |
| ∑ | ||
| i = 0 |
Vérifiez que Vn converge vers e = exp(1) = 2.71828...
Exercice 7 : Figures en mode texte (niveau 1)
a) Ecrivez un programme qui affiche les valeurs 1 à 9 en ligne, à l'aide d'une boucle for:
123456789
b) Modifiez le programme pour qu'il affiche 9 lignes similaires, à l'aide de 2 boucles for:
123456789 123456789 . . . 123456789
c) Comment modifier le programme pour qu'il affiche un triangle ?
1 12 123 1234 12345 123456 1234567 12345678 123456789
d) Modifiez une dernière fois votre programme, pour qu'il affiche une pyramide inversée:
1
12
123
1234
12345
123456
1234567
12345678
123456789
Exercice 8 : Triangle (niveau 2)
Utilisez des boucles afin de construire un triangle isocèle formé par le caractère étoile (*). Affichez-en n lignes, où n sera entré au clavier par l'utilisateur.
Exemple: pour n = 5 :
*
***
*****
*******
*********
Exercice 9 : Devoir 3 du MOOC (niveau 2)
Les devoirs du MOOC, même s'il ne sont pas notés pour vous, sont un excellent moyen de vous entraîner (notamment en vue du mini-projet). Vous pouvez les soumettre à un correcteur automatique (autant de fois que vous le souhaitez) et recevoir un feedback. Cette semaine il est recommandé de réaliser le devoir de la semaine 3 pour vous entraîner à la formulation de traitements répétitifs.