Série 14 :
Révisions
Buts
Pour finir le semestre, nous vous proposons trois exercices en relation avec la partie théorique du cours et qui vous permettront d'exercer vos acquis de programmation. Vous n'aurez évidemment pas le temps de tous les réaliser et le corrigé est d'emblée fourni pour vous permettre de réviser. Choisissez-en un à réaliser selon votre niveau et intérêt (et plus si vous avez le temps)!Une façon simplifiée de configurer QTCreator vous est proposée dans cette série. Inspirez-vous de la vidéo de la semaine 4 en utilisant cette fois l'archive serie14.zip.
Exercice 1 : LIEN PARTIE THÉORIQUE : moyenne mobile (niveau 1)
Cadre général
Dans la partie théorique du cours, vous avez vu le filtre à moyenne mobile d'un signal continu (calcul par une intégrale). Ici, nous vous propopons de voir comment calculer la moyenne mobile « discrète » d’un signal échantillonné, c.-à-d. une approximation (par somme de Riemann) de la version continue vue en partie théorique.
Un signal échantillonné n'est qu'un ensemble fini de valeurs, un tableau de valeur en programmation. Sa moyenne mobile n'est autre que la moyenne d'un nombre fixe de ces valeurs.
Soit Tc ce nombre fixe de valeurs sur lesquelles ont veut faire la moyenne (c'est un nombre entier). Par exemple, Tc = 3.
La valeur à l'échantillon n (c.-à-d. au temps t = n Te) du filtre à moyenne mobile est définie comme la moyenne des Tc valeurs précédentes du signal Y :
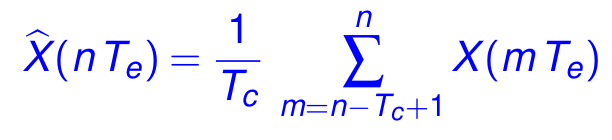
Par exemple, si X vaut : 15.1, 14.8, 13.7, 12.6, 13.8, 14.1, et que Tc = 3, alors la valeur du signal filtré vaut :
14.53 (moyenne de 15.1, 14.8 et 13.7),
13.70 (moyenne de 14.8, 13.7 et 12.6),
13.37 (moyenne de 13.7, 12.6 et 13.8),
et 13.50 (moyenne de 12.6, 13.8 et 14.1).
Implémentation
Un signal échantillonné sera donc simplement représenté comme un tableau de valeurs. La fonction « _filtre à moyenne mobile » prend alors simplement en paramètres le signal d'entrée (tableau de valeurs) et la taille de la fenêtre (Tc) et retourne le signal filtré, c.-à-d. un autre tableau de valeurs.
A noter que dans la définition précédente, la première valeur du signal filtré ne peut être fourni qu'après avoir eu au moins Tc, les valeurs précédentes n'étant pas définies.
Pour simplifier, nous allons ici décider que le signal filtré à la même taille que le signal d'entrée et que ses Tc - 1 valeurs initiales sont identiques à celle du signal de départ (choix arbitraire simple à implémenter). Voir l'exemple ci-dessous.
Implémentez la fonction qui effecture ce filtrage à moyenne mobile, puis, pour plus facilement exploiter le résultat de votre programme, implémentez également une fonction qui prend deux tableaux de valeurs en argument et les affiche alignés comme dans l'exemple ci-dessous.
Exemple
Si par exemple le signal échantillonné de départ a les valeurs :
15.1, 14.8, 13.7, 12.6, 13.8, 14.1, 14.5, 14.8, 15.0, 15.1, 15.5
alors le programme devra afficher :
# signal moving average 15.1 15.1 14.8 14.8 13.7 14.5333 12.6 13.7 13.8 13.3667 14.1 13.5 14.5 14.1333 14.8 14.4667 15 14.7667 15.1 14.9667 15.5 15.2
Dessin des courbes avec gnuplot (optionnel)
Le format utilisé pour l'affichage permet d'utiliser un logiciel de dessins de courbes appelé gnuplot, utilisable sur les VMs, de la façon suivante:
-
Lancez votre programme en redirigeant sa sortie dans un fichier avec le signe
>:./moving_average > resultat.txt(vous pouvez alternativement copier-coller les affichages de votre programme dans un fichier resultat.txt) -
Lancez
gnuplot -
Donnez lui la commande :
plot "resultat.txt" u 1 w linesp t "signal", "resultat.txt" u 2 w linesp t "moyenne mobile"
Vous devriez alors avoir la figure suivante à l'écran :

Note : si la légende n'est pas au bon endroit, dans gnuplot donnez simplement la commande :
set key bottom right; replot
Exercice 2 : LIEN PARTIE THEORIQUE : calcul d'entropie (révision sur les tableaux/fonctions, niveau 2)
On se propose ici de calculer l'entropie
- d'une chaîne de caractères telle que définie dans le cours d'ICC;
- plus généralement, d'une distribution de probabilité.
Distribution de probabilité
Une distribution de probabilités est simplement un tableau de nombres réels compris entre 0 et 1 et dont la somme est 1.0
Une distribution de probabilité sera donc simplement pour nous un tableau de double.
Entropie d'une distribution de probabilité
L'entropie d'une distribution de probabilités est l'opposé de la somme de ses valeurs multipliées par leur logarithme. Si l'on veut l'exprimer en bits, on prendra le logarithme en base 2 :

Définissez une fonction entropie qui calcule l'entropie d'une distribution de probabilités.
Attention à traiter correctement le cas p=0, pour lequel p log(p) vaut 0.
Entropie d'une chaîne de caractères (définition ICC)
Dans le cours ICC, nous avons défini l'entropie d'une chaîne de caractères comme l'entropie de la distribution de probabilité empirique, i.e. la distribution de probabilité résultant du décompte du nombre de chacune des lettres dans cette même chaîne.
Il nous faut donc commencer par calculer cette distribution. Définissez pour cela une fonction calcules_probas qui reçoit une chaîne de caractères et retourne la distribution de probabilité de ses lettres : pour chacune des lettres, on compte le nombre de fois qu'elle apparaît dans la chaîne puis on divise par le nombre total de lettre.
Pour rendre cette fonction un tout petit peu plus générale :
- on ajoutera un paramètre booléen supplémentaire qui, lorsqu'il est
true, prendra en compte également les espaces (i.e. 27 lettres) alors que sinon le calcul est fait comme dans le cours ICC en ignorant les espaces ; - on ignorera la casse (i.e. la différence majuscule, minuscule) : utiliser pour cela la fonction
toupper()de la bibliothèquecctypequi retourne la version majuscule (ou lui-même) d'une lettre (alphabétique) reçue en paramètre ; on utilisera par ailleurs au préalable la fonctionisalpha(de la même bibliothèquecctype) pour déterminer si un caractère donnée est une lettre de l'alphabet ou non.
Pour calculer cette distribution de probabilité empirique, je vous conseille de tout d'abord créer un tableau de taille fixe de 27 nombre pour compter le nombre d'occurrence de chacune des vingt-sept lettre. Utilisez ensuite ce tableau pour construire une distribution de probabilité avec uniquement les lettres qui apparaissent, i.e. les probabilités non nulles (cf exemple ci-dessous).
Terminez en définissant une fonction entropie qui reçoit en paramètre une chaîne de caractères et retourne son entropie (i.e. l'entropie de sa distribution empirique des lettres).
Tests
Voici quelques entropies qui vous permettrons de tester votre code :
| distribution | entropie (en bit) |
|---|---|
| { 0.0, 0.1 } | 0 |
| { 0.3, 0.7 } | 0.881291 |
| { 0.5, 0.5 } | 1 |
| { 0.1, 0.2, 0.3, 0.4 } | 1.84644 |
| { 0.25, 0.25, 0.125, 0.0625, 0.0625, 0.0625, 0.0625, 0.0625, 0.0625 } | 2.875 |
Et pour rappel (cf cours ICC), l'entropie de la chaîne « IL FAIT BEAU A IBIZA », en ignorant les espaces, est de 2.875 bit, sa distribution de probabilités étant la dernière donnée ci-dessus.
Exercice 3 : LIEN PARTIE THÉORIQUE : codes de Huffman (structures, tableaux, fonctions, ..., niveau 3)
Le but de cet exercice est de réaliser des codes de Huffman de textes. Le principe du code de Huffman (binaire) est assez simple : il consiste à regrouper les deux « entités » les moins probables à chaque étape; une « entité » étant soit une lettre de départ, soit un groupe d'entités déjà traitées (une, deux, trois, ... lettres déjà traitées).
Le plus simple est peut être de commencer directement par l'algorithme lui-même à un niveau d'abstraction assez haut (approche descendante) :
à partir de la distribution de probabilité initiale des lettres (leur compte), on va, de proche en proche tant qu'il nous reste plus que deux « entités » à traiter
rechercher les deux entités les moins probables ;
-
ajouter le symbole
'0'devant tous les codes déjà produits pour la première de ces deux entités ; -
ajouter le symbole
'1'devant tous les codes déjà produits pour la seconde de ces deux entités ; -
fusionner ces deux entités en une nouvelle entité, dont on calcule la probabilité : somme des probabilités des deux entités fusionnées;
pour cela on écrasera une de ces deux entités par leur fusion et on supprimera l'autre.
Notez qu'on a donc une entité de moins à chaque fois (la fusion supprime les deux entités, mais n'en rajoute qu'une seule nouvelle).
Il nous faut donc représenter ces « entités » (et un ensemble d'entités). Je vous propose de le faire de la façon suivante :
-
une « entités » est simplement un groupe de lettres avec sa probabilité ;
-
le groupe de lettres peut simplement être représenté par la liste des positions de ces lettres (voir ci-dessous) ;
-
au départ, ces entités correspondent simplement aux lettres du mot avec leur probabilité.
Nous aurons aussi besoin de représenter le code lui-même. Un code est une bijection entre les mots à coder et leur code. La bonne structure de données pour représenter cela est ce que l'on appelle des « tables associatives », que nous n'avons pas encore vues (2e semestre). A ce stade du cours, nous vous proposons donc simplement de représenter le code comme un tableau dynamique de structures contenant:
- le mot à coder (type « chaîne de caractères ») ; dans les exemple du cours, c'est simplement une seule lettre, mais on pourrait généraliser ;
- la probabilité correspondante ;
- le mode de code correspondant (type « chaîne de caractères »)).
Prenons un exemple (cf cours ICC) :
supposons que l'on veuille coder la phrase « JE PARS A PARIS »
On commencera par créer un « code » (il n'est pas complet à ce stade, tous ses mots sont vides) contenant par exemple (ordre de lecture ici, mais vous pouvez changer cet ordre, bien sûr):
-
"J", probabilité :1./12., mot de code vide; -
"E", probabilité :1./12., ...(mot de code vide); -
"P", probabilité :2./12., ...; -
"A", probabilité :3./12., ...; - etc.
-
"I", probabilité :1./12., mot de code vide.
Une fois ce « code » (mots vides) créé, on pourra créer la version initiale de la liste d'« entités » nécessaires pour l'algorithme décrit plus haut (ordonnée à nouveau ici dans l'ordre de lecture, mais vous pouvez choisir un autre ordre):
-
indices :
0, probabilité :1./12.;
cette entité représente la lettre"J", lettre à la position0dans le « code » (mots vides) précédemment créé ; -
indices:
1, probabilité :1./12.; -
indices:
2, probabilité :2./12.; - etc.
-
indices:
7, probabilité :1./12..
Pour l'instant cette liste d'« entités » ne semble pas très intéressante et semble faire double emploi avec le code : c'est normal : le code de Huffman commence par les lettres seules.
Mais dès la première étape de codage, cela va changer : on commence par regrouper les deux moins probables, disons par exemple le "J" et le "E" (les deux premiers moins probables dans l'ordre de lecture, là encore votre choix peut être différent suivant comment vous écrivez l'algorithme, cela ne change rien au final sur la longueur moyenne du code). On aura alors une nouvelle entité :
indices: 0, 1, probabilité : 2./12.;
et la liste d'« entités » devient (elle ne contient plus que 7 éléments):
-
indices:
0,1, probabilité :2./12.; -
indices:
2, probabilité :2./12.; - etc.
-
indices:
7, probabilité :1./12..
Et comme dit au départ de cet exercice : une fois la fusion ci-dessus effectuée (ou même avant), on ajoutera respectivement '0' et '1' à chacun des mots de code correspondants. Dans cet exemple précis, cela à revient à les ajouter à chacun des deux mots de code, vides, de "J" et "E".
Voilà pour les structures de données proposées pour cet algorithme.
Pour l'algorithme lui-même : adoptez (bien sûr !) une démarche très modulaire en introduisant des fonctions pour chacune des tâches élémentaires ; par exemple : compter les lettres, normaliser les probabilités, fusionner 2 entités, rechercher les deux entités les moins probables, ajouter un symbole à un mot de code, construire les entités initiales à partir d'un « code » (mots vides), etc. etc.